Any high school student hoping to enter a university program of studies in chemistry, physics, and mathematics and engineering in the late 1950s, was expected to understand and use the principles of mathematics outlined in this monograph. These were the days of the Soviet-American Cold War when science and engineering courses reigned supreme in a college’s annual catalog.
Brother Arthur stood at the blackboard in front of some 25 Franco-American boys, who had selected to undergo a rigorous learning experience regarding the basic elements of algebra. This mathematical treasure, which had been successfully handed down to these ardent, young minds over the previous two centuries, would, hopefully, become the kingpin of their future success in an engineering-centered society like ours.
Fortunately for us boys, “The Elements of Algebra” written by Leonard Euler (1707 – 1783) represented for Brother Arthur the nuts and bolts of his enthusiastic, teaching career. Never had a craftsman visiting my neighborhood of Centralville shown any more adeptness in manipulating a sachel of special tools to solve a customer’s problem.
The bets were on! Somehow, we might achieve technical parity in competing with Soviet students in the USSR, who had been immersed by the state in challenging fields like physics, chemistry, engineering, and mathematics.
Brother Arthur’s Mathematical Skills and Muscular Attributes
His physical presence in that typical, austere black cassock worn by Marist brothers worldwide made a lasting impression on us boys, his new pupils. He was not someone, who might shrink, in a docile way, from a potential pupil-teacher misunderstanding in the classroom. He must have had access to a bodybuilding gym in the area as the bulging, muscular ripples in his habit clearly showed.
Brother Arthur stood out among the other staff members of that educational institute. A person with a religious dedication to his Franco-American brethren could, at the same time, be a no-nonsense sheriff in the classroom. In his case, a confrontation might be tumultuous.
Euler’s Elements
The history of algebra, an Arabic word, goes back to the days of Euclid and the ancient Babylonians and Egyptians. Concepts like addition, subtraction, division, and multiplication plus equations expressed in symbolic form were also formulated by sages in India and the Islamic world.
Fortunately for us, Brother Arthur never put us through the long and tedious, historical development of this field of mathematics. In contrast, his central theme focused on the refinements to these methods that were introduced by Euler and also Carl Friedrich Gauss (1777-1855) over the next two centuries.
Examples from Everyday Life
Consider the number of eggs on the kitchen counter. There are: 3 eggs plus 6 eggs, so the number of eggs equals 9 or 3 + 6 = 9.
If, instead, you were counting the number of lobsters on the counter, you would have: 3 lobsters plus 6 lobsters, so the total number of lobsters would equal 9. Pretty easy, yes?
If you understand this bit of thinking, then you, already, are a good candidate for doing high school algebra! Note, in passing: you also realize that the order of counting lobsters or eggs gives the same result, i.e., 3 + 6 = 6 + 3. The same rules hold in algebra for any two numbers, so that a + b = b +a where a and b are ordinary numbers.
Surprised? You should not be. Every day, you use this type of calculation in making decisions to run your life and business. You, also, use this type of thinking in preparing a nice batch of creamy batter using your fabulous Quebec crepe recipe.
Carpentry Example
Joe needs two pieces of 2×4 boards to match in length. The longer piece is 96 inches (eight feet) long while the shorter one is 85 inches long. How much of the longer piece must he cut to get two equal length pieces? This calculation you could do in your head, but here is how it would be expressed in algebra:
96 – x = 85 or, after subtracting 85 from each side of the equation and also adding x to each side, we find:
96 – 85 = 11 = x
Again, the unknown length is 11 inches, which you could easily have found in your head. However, the formal approach using the rules of algebraic manipulations are given here to help the pupil in dealing with more complicated situations.
A more difficult problem follows.
Joe is now building a rectangular picture frame for his daughter, Sarah. The distance around the frame is called the periphery, P, which is given, in general, by:
P = 2 (l +w) where “l” is the length and “w” is the width of the frame.
If his daughter wants the length, “l”, to be 3 times the width, “w”,. How do we use algebra to express P, the periphery?
First, we can, now, write that P = 2(3w + w) = 2(4w) = 8w
but, if she needs the distance around the frame to be 48 inches, then we conclude that
P = 48 = 8w or w = 6 inches, so the length, “l” must be:
length = 3w = 3(6) = 18 inches.
Check your answer:
In general, P = 2(l + w) and, in this case, we have P = 2(18 +6) = 2(24) = 48
It all checks out!
Symbols used in Algebra and More on Equations
In all of life, certain rules and regulations need to be accepted by all participants to ensure a free flow of ideas and actions, which lead to results. Hockey, football, and baseball are sports played under the guidance of accepted rules. In contrast, algebra and mathematics allow us to represent symbolically the relationships between different quantities, which appear as interrelated statements. A simple example follows.
Consider the following statements. The quantities “a” and “b” are the numbers “3” and “4”, respectively. Therefore, we could write: “a” is 3, and “b” is 4. So, the sum of these two numbers is 7. In algebra, these ideas would be simply expressed as: :
a = 3; b = 4, so, the sum = a + b = 3 + 4 = 7
Some of the standard symbols used in algebra include: +, -, =, >, <, and many more.
A complete list of common algebraic symbols can be found at the web site called: Symbols in Algebra. There was much to know before a high school boy like myself might participate in a national algebra runoff contest. However, I could pride myself on coming in second in a local French spelling bee contest, but this minor victory never even made the local papers. Fame and glory were fleeting in my high school years.
“Rome was not built in a single day.” This gracious comment coming to us from the Christian catacombs of ancient Rome carried me through one more encounter with the real world.
But, to his credit, the stern but religiously patient Brother Arthur never imposed the full flagellation of the complete list onto the trembling shoulders of his captive brood.
In algebra, we often run into equations and then try to find roots to these equations. Sometimes, there is more than one unknown quantity. See below.
Example on Budgeting at a Yard Sale
Now, a slightly more complicated situation follows. Your cousin, Karen, has accepted to spend some money at a yard sale to raise funds for a charity. One of the items that has caught her attention costs “x” dollars and a second item costs “y” dollars.
However, this yard sale has a hidden motive, i,e, to encourage visitors to use their high school algebra talents to solve the following dilemma:
The two numbers, x and y (above), relate to one another through the two equations given below:
5x + 2y = 9 Eq(1)
3x – y = 1 Eq(2)
Here, we notice that we can eliminate the unknown, “y” by first multiplying the second equation by 2 to get:
6x -2y = 2 Eq(3)
Next, we add Eq(1) to Eq(3) which gives us:
5x + 6x = 9 + 2 or
11x = 11, so, x = 1.
Finding the value of y is now easy.
From Eq(1), we have:
5(1) +2 y = 9 or, 5 + 2y = 9
So, adding negative 5 to each side of this equation, we find:
5 +2y -5 = 9 -5 = 4, or 2y = 4
and, therefore, y = 2.
Finally, if Karen has $5.00 to spend at the yard sale, she could easily do so, using these calculations as a guide. As a matter of fact, she could afford to get two items labelled y and also one item labelled x.
Summary Comments on “row reduction” and Gaussian elimination
The approach used in solving simultaneously the two equations given above is called “row reduction” or Gaussian elimination. Carl Friedrich Gauss gets much of the credit for introducing this sweeping approach to solving sets of n independent, simultaneous equations in n variables often found in engineering and science projects. More comments on Gauss and his work will be found in a later section.
Note in passing: The most enthralled student of algebra 1 presented here, would want to pursue this type of investigation by next plunging into the n-dimensional world of matrix algebra, which any large scale project manager is expected to encounter in his/her professional career. However, this stuff is not for the timid!
Contractor’s Problem: A typical word problem
Farmer Jones has three identical barns on his property in the woods of Dracut, Mass. Also, Jack and Jill are each independent contractors in the area.
At first, the good Farmer Jones asks Jack to paint the first barn, which he completes in 40 hours.
Next week, Jill is hired to paint the second barn, which she completes in only 35 hours.
Finally, the farmer needs to have his third barn also painted and he wishes to have both Jack and Jill work on this last project together without getting into each others way.
How long would it take to have this last barn painted?
Note:
At Jack’s rate of work, the job is done in 40 hours.
At Jill’s rate of work, the job is done in 35 hours.
The team rate of work is what?
Note that, in general,
Job cost = worker rate multiplied by hours on the job.
In this case, Job = (Job/40 + Job/35)x
where x is the time in hours to finish the job while working together.
Basically, this says that Job = Job(1/40 + 1/35)x or
1 = (1/40 + 1/35)x, so by multiplying each side by 40, we find:
40 = (1 + 40/35)x = (1 + 8/7)x = ( 7 + 8)/7(x)
7(40) = 15x or 7(8) = 3x and, finally, x = (7)(8)/3 = 56/3 = 18.6667 hours.
Note that if each painter worked at Jill’s rate, then the time to complete the job would be the following:
Job = Job(1/35 + 1/35)x = Job(2)(1/35)x
so, therefore, 1 = 2(1/35)x
or
35 = 2x, so x = 35/2 = 17.5 hours or half of Jill’s rate while she was working alone.
This checks out OK. In this last case, Jack would need to speed up his output rate to match that of Jill’s.
The Genius that was Carl Friedrich Gauss
He was called by many “the greatest mathematician since antiquity”. In addition to making a fundamental contribution to solving a group of simultaneous linear equations (see: Gauss-Jordan elimination method), he also formulated one of Maxwell’s four laws of electricity and magnetism. In recognition, for this latter piece of genius in E&M theory, that law, today, is called “Gauss’s law”.
How does this type of mind function? That is a question of physiology, which remains a mystery, but an anecdote from his early years as a pupil in a Göttingen classroom tells the story.
Apparently, his school teacher had interrupted his regularly planned set of instructions to the class so as to quietly discuss an important issue with a visiting schoolmaster outside the classroom. So as to keep the pupils well occupied during his absence, the teacher asked that they spend some time adding up all the numbers from 1 to 100.
The little Gauss boy came up with the right answer in a flash. The sum of those 100 numbers came up to be 5050. How did he do it so fast?
In doing the problem the old-fashion way, a student would add 1 to 2 to 3 to 4, to 5, etc. up to 100. That would be 99 separate additions, which would be very time-consuming and boring, too.
A much faster approach would be to first realize that there is symmetry in this arrangement of consecutive numbers forming the sum. In this case, it is simple. Starting with the number 1, every following number is one larger than the previous number. This realization is how Gauss arrived at counting so fast.
Consider, first, a simpler problem of adding the numbers from 1 to 10. The sum would be expressed as:
Sum = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 or
Sum = 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1
By adding these two sums together, we find that:
2Sum = 11 + 11 +11 +11 + 11 + 11 + 11 + 11 +11 +11 Therefore:
2Sum = 10(11) Therefore:
Sum = 5(11) = 5(10 + 1) = 50 + 5 = 55
which you can easily verify by adding 1 to 2 to 3 ….to 9 and to 10. But, in a more mathematically rigorous fashion, we might consider Gauss’ more elegant approach to problems of this nature. See next section.
Finite Series – Looking at Life in a Different Way
If we hope to learn and use the mathematical tools developed for science and engineering since the days of Pythagoras (about 570 BC – c. 495 BC) in Greece, it would behoove us to peek into the brilliant mind of our little German friend, Carl, as he was toying with sums of many, many numbers after he had solved some financial accounting problems for his dad.
Certainly, we cannot hope to replicate his sweeping and elegant approach to difficult problems, but, maybe, just maybe, his clarity of thought just might rub off on our struggling brain cells. So, let’s get started.
Consider the following sum from the first number = a to the final number = l where the constant increment number = d.
Therefore, we find the Sum equal to:
Sum = a + (a + d) + (a + 2d) + (a + 3d) + (a + 4d) + …… + (a + (n -2)d + l
and, also, we can write this sum starting from the last number, l, and counting downward.
Sum = l + (l – d) + (l – 2d) + (l – 3d) + …….. + (l – (n-2)d) + a
Note that if we add these two expressions for the Sum, we obtain:
2Sum = (a + l) + (a + l) + (a + l) + (a + l) + ….. + (a + l) + (a + l)
We find that there are n terms of (a +l) on the right-hand side. Finally, we obtain the general expression given below.
Sum = n(a + l)/2
where, in the series, the first term = a; the last term =l, and the number of terms is n. Note that the integer constant spacing between each term in the series is d. In the classroom, Gauss was dealing with the case where d = 1.
Usually, an experimenter or engineer using a mathematical expression such as this one wishes to prove the validity of a general result by first testing predicted results with actual lab results.
Verification of results – Expression is: Sum =n(a +l)/2
Case#1:
a = 7, l =13 and n = 7 where n = number of terms
Sum = 7 + 8 +9+10+11 +12 +13 = 15 +19 + 11 +25 = 15 + 30 + 25 = 70
Easier way gives:
sum = 7(7 + 13)/2 = 7(20)/2 = 7(10) = 70 OK!
Case#2:
a = 1, l = 1 and n = 1 This is a special case where the first term and the last term are the same.
Sum = 1
Easier way gives:
Sum =(1)(1 + 1)/2 = (1)(2)/2 = 1 OK!
Case#3:
a = 13, l = 27 and n = 8
Sum = 13 + 15 + 17 + 19 + 21 + 23 + 25 + 27 = 28 + 36 + 44 + 25 + 52 = 160
Easier way follows:
Sum = 8(13 +27)/2 = 4(40) = 160 OK, this checks out.
Conclusion: Using Gauss’ formula for the sum of n numbers where the first number = a and the last number = l is, indeed, given by the simple expression: Sum = n(a + l)/2
QED: quod est demonstrandum or “that which was to be demonstrated”
Quadratic Equation and its General Solution
So far, the interaction between linear equations have been discussed, but how would a student find answers to a more complex equation where the unknown quantity, “x” is raised to a power of n?
Answer: He/she could not do this since the general expression holds only for the case where n = 2. There exists no general formula for finding roots to similar equations where the unknown quantity, x, is raised to any other number.
Consider the case where:
ax2 + bx + c = 0
But, in the special case where c = 0, then we find:
ax2 + bx = x(ax + b) = 0
Therefore, we are then left with the two roots being: x = 0 and x = -b/a
The derivation of the general formula is given at this website
Note that: Brother Arthur carefully went through many steps of similar additions and subtractions of equal quantities from each side of the equation: ax2 + bx + c = 0 to prove his point.
I was very impressed with the efficiency and elegance that he displayed in this proof. Such mathematical dexterity encouraged me to believe that, maybe, there is underlying sanity and truth in our day-to-day world of downtown Lowell.
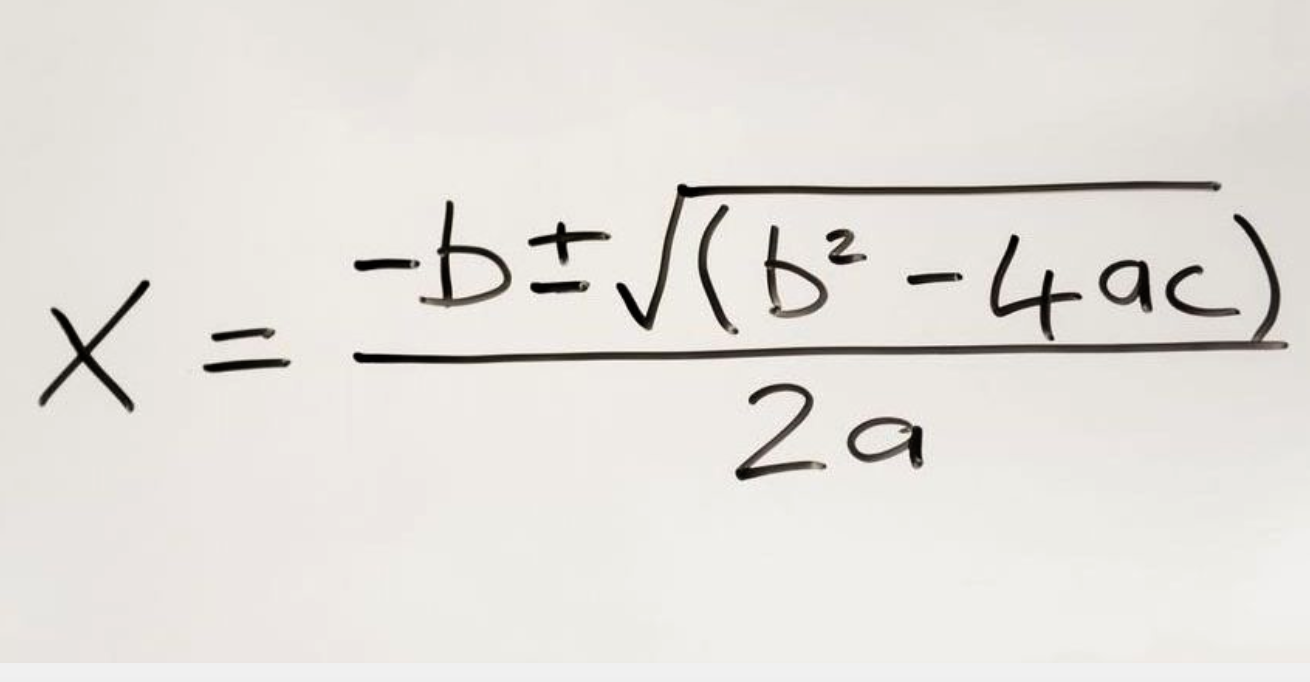
Euclid’s Elements on Geometry, the Pythagorean equation and Trigonometry
Up to this point, I have been remiss in not dealing with the world of Euclid (325 – 265 BC) and Pythagoras (570 ~490 BC), and the other ancient Greek mathematicians, who successfully applied their theoretical and practical skills to the construction of structures like the Roman Colosseum, the Trajan Market, the Parthenon, Acropolis in Athens, in addition to Temple of Artemis, Corfu, Pont du Gard, and others. My oversight is egregious but, hopefully, this architectural sin will be successfully handled in the next section.

